This paper was published in Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering book series (LNICST,volume 126) in 2012
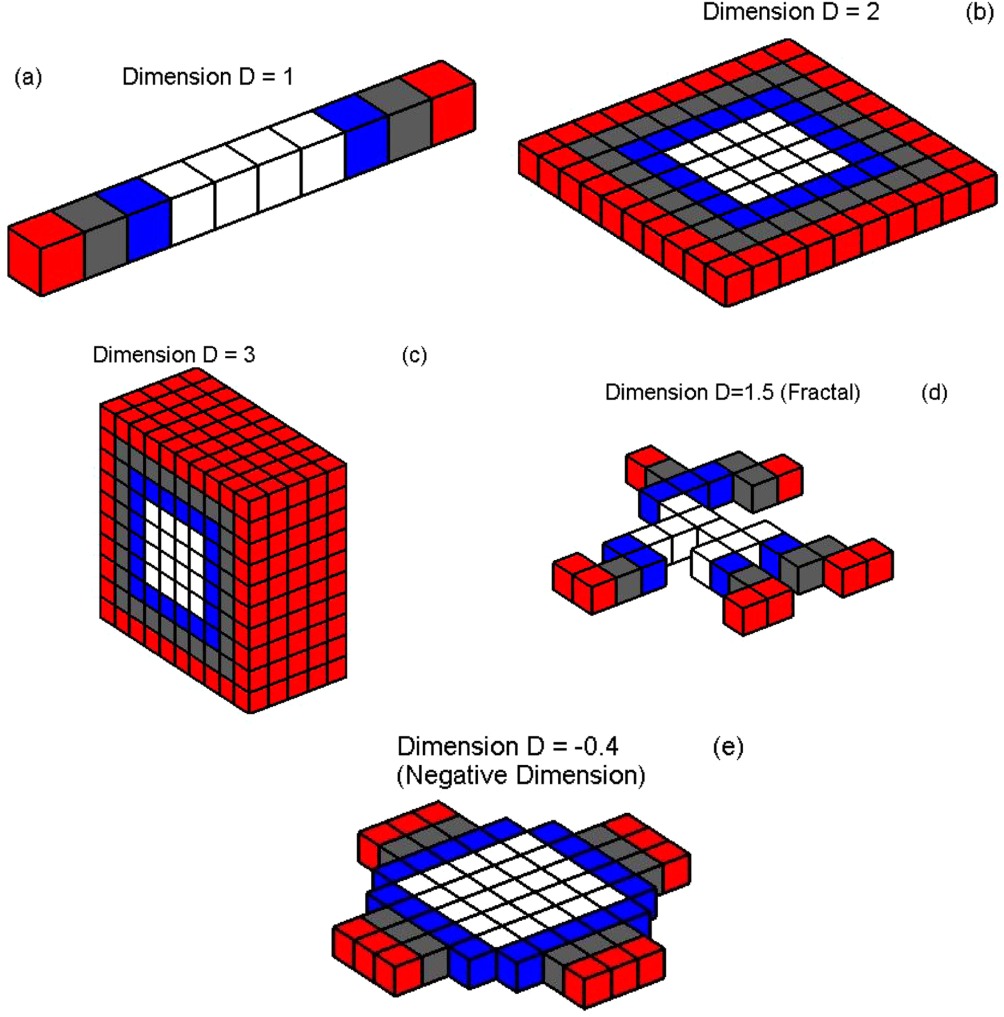
In sets with a fractal dimension greater than 1, the average number of neighbors increases with distance. For that reason spherical pulses propagate outward in systems with nearest neighbor interactions. In sets with a negative fractal dimension, such as the set of individual coordinates of a population of a small city, the average number of neighbors decreases with distance in a precise way relating the number of neighbor to the fractal dimension of the set. We study the propagation of diffusive pulses and waves on such sets. We find that on sets with negative fractal dimension, the velocity of pulse peak is negative (i.e. the median radius of circular pulses decreases as a function of time). Eventually the pulse broadens and disappears. We discuss applications in physical systems, such as the spreading of heat and sound, as well as applications in social systems, such as the spread of infectious diseases and the spread of rumors.
If the elements are sorted in terms of their distance from the center of mass, the largest group is the group near the surface of the object. Therefore for the largest group of elements the object appears to be D-1 dimensional.
In order to view the entire paper, please visit Springer's website.