This paper is a research manuscript that I wrote in undergrad.
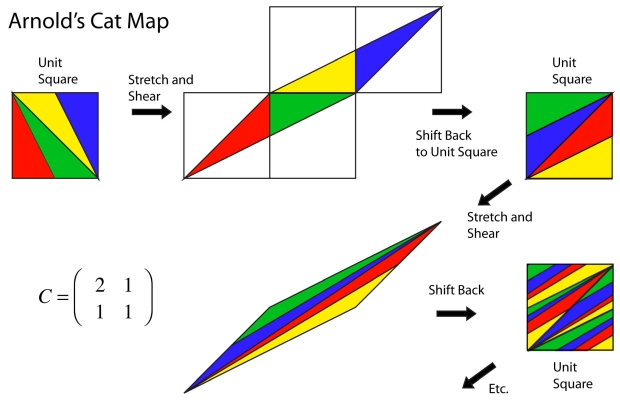
A discrete dynamical system known as Arnold’s Discrete Cat Map (Arnold’s DCM) is given by (xt+1, yt+1) = (xt + yt, xt + 2yt) mod N, which acts on a two-dimensional square coordinate grid of size N ×N. The defining characteristic of this map is that it has the property that when the N × N grid is a picture whose pixels are assigned (x, y) coordinates, the map scrambles the picture with each iteration. After a finite number of iterations, the picture is restored to its original shape and order. The number of iterations needed to restore the image M, has a mysterious dependence on N. This period, as we will find out, is directly related to the divisibility of the Fibonacci numbers. We will exploit this property to show that, for any N, an image is not dense in itself. In the second half of the paper, we build on the work of Chen, Mao, and Chui to extend the DCM to three dimensions. Finally, we define the generalized n dimensional DCM by introducing the idea of a “matrix union”.
What would a three dimensional analog to the 2D DCM look like? Certainly, the mapping would have to act on an N×N×N cube.