This paper was published in the journal International Mathematics Research Notices in 2012
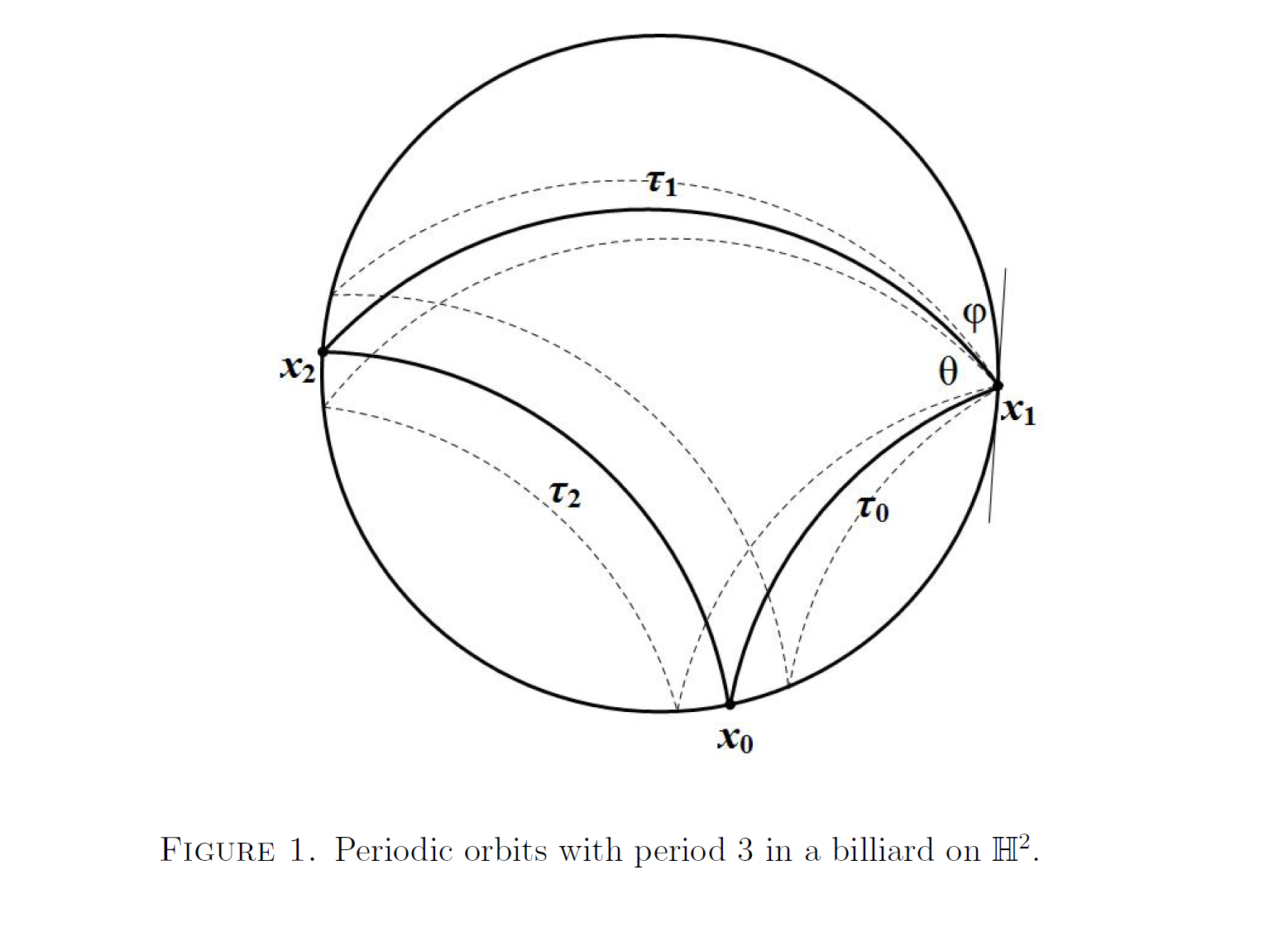
An approach due to Wojtkovski, based on the Jacobi fields, is applied to study sets of 3-period orbits in billiards on hyperbolic plane and on two-dimensional sphere. It is found that the set of 3-period orbits in billiards on hyperbolic plane, as in the planar case, has zero measure. For the sphere, a new proof of Baryshnikov's theorem is obtained which states that 3-period orbits can form a set of positive measure if and only if a certain a natural condition on the orbit length is satisfied.
While the spherical as well as Euclidean case has been treated previously, our result for the billiards on hyperbolic plane is a new one.
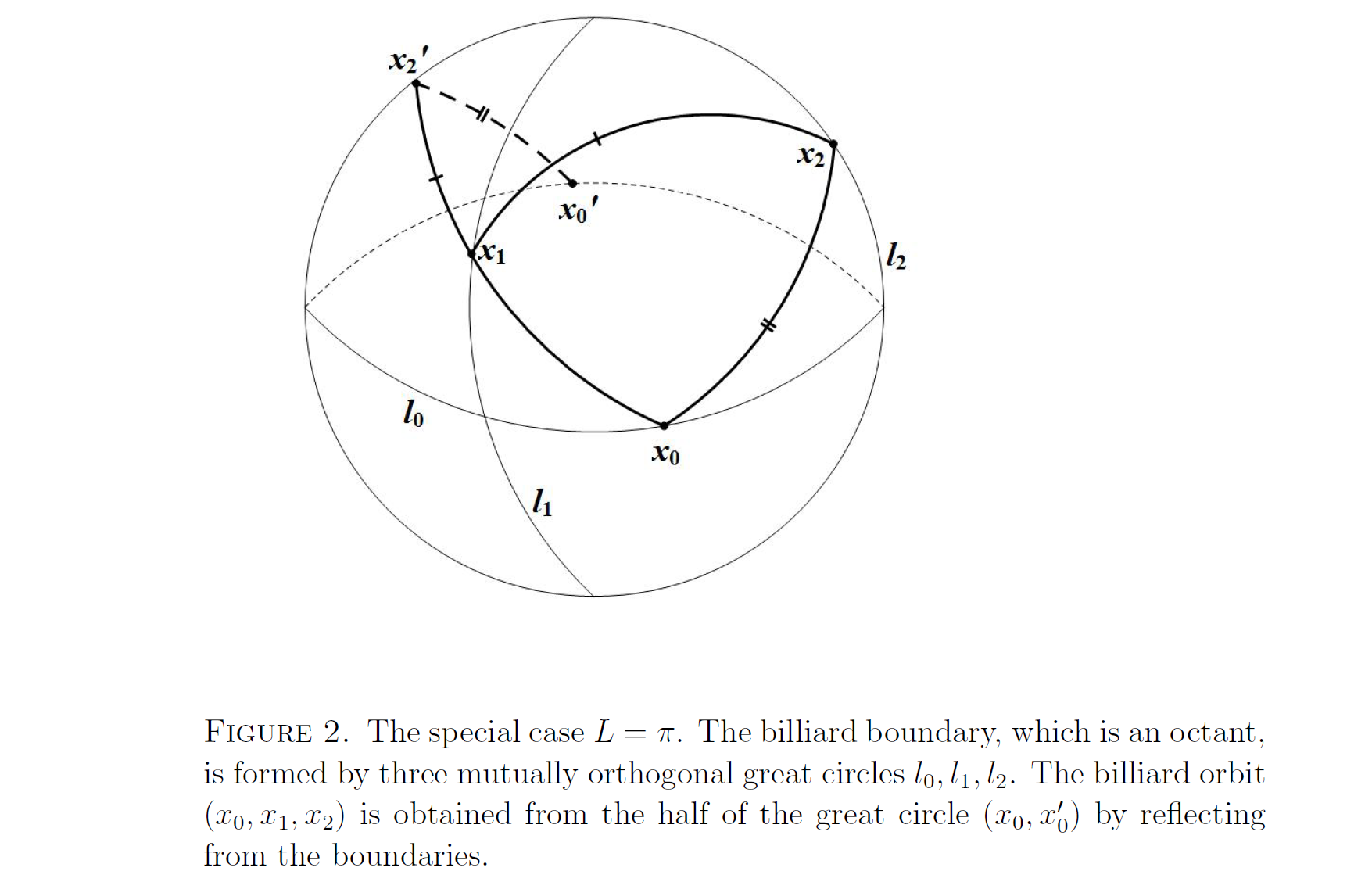
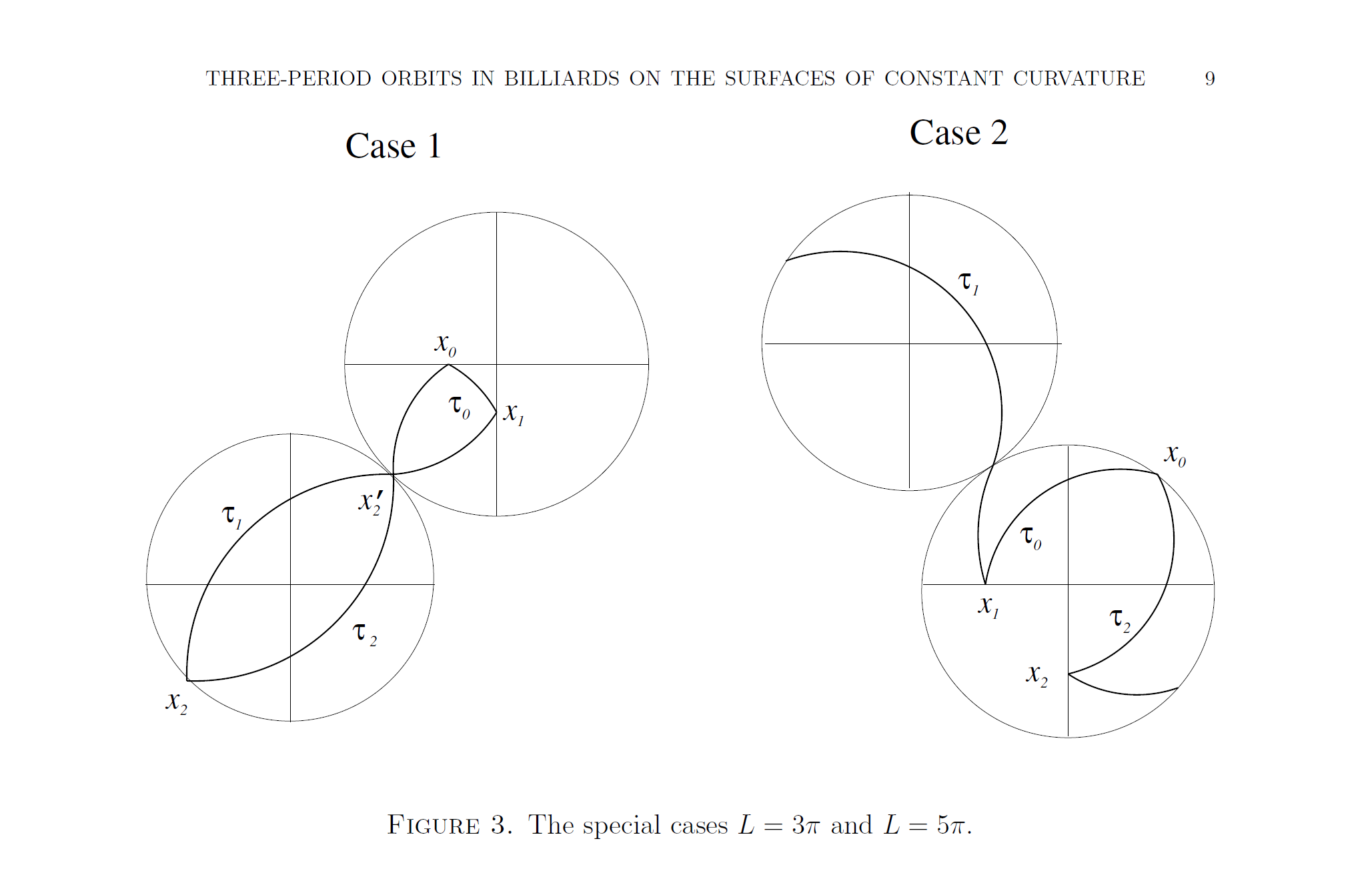
This article provides a unified approach, based on the Jacobi fields, to study open sets of 3-period orbits in billiards on manifolds with constant curvature. Specifically, we consider spherical and hyperbolic cases. While the spherical as well as Euclidean case has been treated previously, our result for the billiards on hyperbolic plane is a new one. Billiards on manifolds of constant curvature have been studied earlier in [7], [9]. In [9], billiard domains on the sphere, containing open sets of periodic orbits, have been constructed. In [2] and in this article, the main goal is to assure that except for those special cases, 3-period orbits have zero measure.